はじめに
最近の人工知能(AI)ブームから、人工知能の実装を支える基盤技術である機械学習にも注目が集まってきています。みなさんは機械学習についてどのようなイメージを持っていますか? 世間一般では、機械学習はコンピュータに人間同様の学習能力を獲得させる技術であると、ざっくりと捉えられていると思います。
これまで物事の良し悪しなどの判断は人間が行う仕事でしたが、データが豊富に揃う環境、いわゆるビッグデータの環境が整うことにより、大量なデータを背景にした判断法を機械に学習させることで、このような判断自体を機械に任せようという動きが出てきています。例えば、写真に写っているものが猫であるか否かの自動判定、または、検査データをもとにした病気の自動診断が挙げられます。
機械に判断を任せるという試みが検討されている背景には、判断の責任を機械に押し付けるというよりも、むしろ機械ならば客観的で合理的な判断を下してくれるのではないかという期待があります。本稿では簡単な例を用いて、データに基づく機械による判断の枠組みについて確認していきます。
データからの判断
ある患者が病気かそうでないか、写真に写っているものが猫であるか否か、のように、二者択一の選択肢を選ぶような判断を2値分類と呼びます。
今回は30名の学生の英語と数学の試験点数のデータを例に、機械学習における分類、つまり、データによる判断がどのように行われているかを確認します。図1は、横軸に英語、縦軸に数学の得点をとり、各学生の得点をプロットしたものです。
図1 試験結果
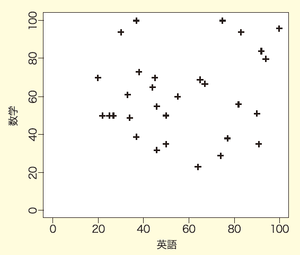
いま、この試験の合計得点が120点以上のときに合格とする場合、合否判定の式は「英語+数学≥120」と表せます。同じデータを使って図示したものが図2です。合格者は○、不合格者は×でプロットしており、赤線よりも上の部分にプロットされた者は合格、赤線よりも下にプロットされた者が不合格になります。
図2 合格基準が120点
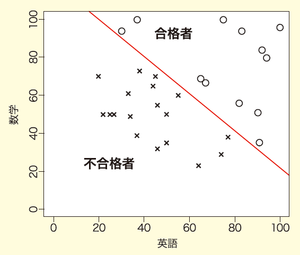
このように、合格者と不合格者を直線で完全に分類できることを「線形分離可能」と呼びます。
もう一つ、これまでと同じデータを使って新しい合格基準を適用した例、図3を見てみましょう。
図3 新しい合格基準
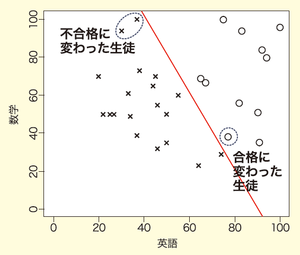
図2では合格していたにもかかわらず図3では不合格になった学生が2名、不合格から合格に変わった学生が1名います。どうやら、英語の得点を重視し、数学の点数が良くても英語の点数が悪い学生は不合格、数学が悪くても英語ができていれば合格にしたようです。
実のところ図3では、合格基準を「2×英語+数学≥180」にしています。今回も合格基準を直線で表現できているため、「線形分離可能」な例になっています。
まとめると、図2と図3における合格と不合格を分離する境界線はそれぞれ次の式で書けます。
- 図2の場合:
英語+数学-120=0
- 図3の場合:
2×英語+数学-180=0
ここで、横軸に英語、縦軸に数学を割り当てていたので、それぞれをxとyで表し直すと、境界線を示す直線の式はそれぞれ次の式で表現できます。
- 図2の場合:
x+y-120=0
- 図3の場合:
2x+y-180=0
この境界線よりも上に位置する学生は合格、下に位置する学生が不合格と判断しています。
いわゆる機械学習では、データと分類結果のみが与えられた状態で、両者をうまく分類できるような境界線を見つけます。つまり、データから合否判定基準を推測する、または、データと合否結果をもとにして、合否判定基準を学習することを目指します。今回のようにデータが2つの場合には、各学生の得点をxy平面上にプロットし、境界を示す直線の式ax+by+c=0の3つの係数a、b、cをデータから求めることになります。
判断基準の推測 ~データからの学習~
これまでは合格基準が明らかになっている場合について考えてきました。続いて、合格基準が分からない状態から推測する、つまりデータからの学習について考えてみましょう。
図4を見てください。この図における合格者と不合格者を分ける分類基準を推測してみましょう。
図4 合格基準が不明な例1
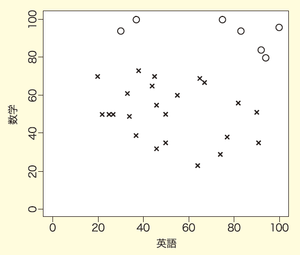
合格基準は1つではなく、いくつかの境界線をひくことができそうです。ここでは、図5に赤色と青色で示したように2通りの合格基準に注目して問題点を確認します。
図5 推測した2つの合格基準
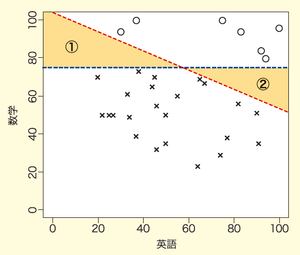
赤線で斜めに引いた境界線も、青線で水平に引いた境界線も、合格者と不合格者を完全に分離できています。つまり、単純に与えられたデータについて、合格基準を推測するだけであれば、赤線も青線も、誤って判定される学生はいないため、何ら問題はないといえそうです。しかしながら、機械学習の目的のひとつとして、データから推測した判断基準を利用して新しいデータの自動判断をさせることがあります。
このように新しいデータの合否判定に利用することを考えると、赤線と青線では大きな違いが生じます。例えば、実際の合格基準が赤線であるにもかかわらず、推測した合格基準が青線である場合には、本来であれば不合格となる領域①に含まれた学生が合格すると誤って推測してしまいます。同様に、本来であれば合格する領域②に含まれた学生は不合格であると誤って推測してしまいます。
つまり、すでに与えられたデータを正しく分類できるだけでなく、新たなデータの分類にも応用できる分類基準が望ましいことが分かります。
次に、少し難しい例を考えてみましょう。図6にはこれまでとは異なる合格基準によって判定した結果をプロットしています。
図6 合格基準が不明な例2
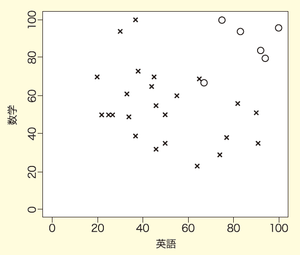
図6を見た感じでは、合格者と不合格者を直線で分類することは難しそうです。このような場合でも、いくつかの機械学習の手法を適用(パッケージングされたプログラムを利用)すれば、何らかの分類境界を推測できます。例えば図7のように、1つは誤った分類となってしまうのですが、その他の学生の合否判定を正しくできるような直線を引くことができます。
図7 直線で推測した合格基準
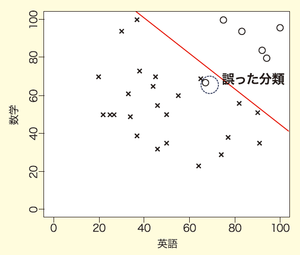
または、今までの前提を崩すことにはなりますが、図8のように直線ではなく、曲線で分類する方法も提供されています(もちろん、直線で分類するよりも高度な知識は要求されますが、困難な計算は機械にすべて任せてしまうという割り切りかたもできます)。
図8 曲線で推測した合格基準
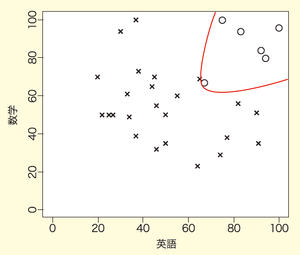
合格者と不合格者を見分ける意味では、図7であっても30名中1名のみ誤っただけですから、必ずしも分類精度が悪いとは言えません。しかしながら、合格基準を推測する観点からは、両者ともによく推測できているとは言い難いかもしれません。
簡単にまとめると、機械学習によってデータを分類する基準を推測する際には、与えられたデータを正しく分類できているか否かという観点だけでなく、新たなデータを当てはめたときにも正しく分類されているかも重要になります。
もやもやする人もいるかと思いますので、最後に種明かしをしておきましょう。図6の合否判定基準は、英語、数学ともに65点以上を取った学生のみ合格するというものでした。つまり、図9で示した右上の赤点線で囲まれた区画に入った学生が合格者になります。
図9 本当の合格基準
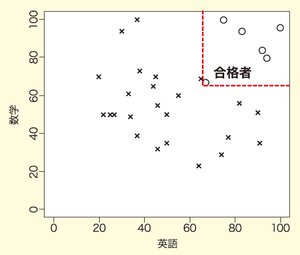
答えを知ってしまえば、非常に簡単な合否判定基準であったと思うかもしれません。ただし、合否判定基準が矩形で与えられているため、図7における直線による合否判定基準も、図8での曲線による合否判定基準のいずれも、本当の合否判定基準をうまく推測できていないように感じるかもしれません(ただし、このように感じてしまう原因は、正答を知ったからであることには注意が必要です)。
おわりに
現実には分類基準が明らかになっていない状態のデータが数多く存在します(そもそも、分類基準が明らかになっていれば、データから推測する必要はありませんね)。加えて、きれいに分類基準が求まらない場合も考えられます。たとえば、直前の模擬試験の結果と、本番の合否結果が得られているときに、模擬試験結果から本番の合否を推測する場合は、模擬試験の結果が良くても不合格する学生(今回の図でイメージすると右上に位置するのに×となる学生)も存在するため、きれいに分類基準が求まらないかもしれません。
簡単に答えが求まらないような問題に直面した時に、あわてずに、しっかりと問題と向き合うためにも、すべてを機械任せにせずに、データを分析するための知識とその経験を積んでおきたいですね。








