コンピュータープログラムが囲碁や将棋のプロ棋士と対等に戦える時代になりました。囲碁のように、高度な戦略的思考を要するゲームでは、コンピューターが人間のトッププレイヤーに勝つことは難しいと言われていましたが、ついにその常識が変わる時代が来たようです。
−−−と、もっともらしく書き始めてみましたが、実は、私は囲碁にはそれほど詳しくありません。そもそも、囲碁における「高度な戦略的思考」とは何なのでしょうか? 囲碁ファンの皆さんからは、喧喧囂囂(けんけんごうごう)の熱い議論が巻き起こりそうですが、コンピュータープログラムの視点で見ると、少し異なった事情が見えてきます。簡単に言ってしまうと、「取り得る盤面の状態」があまりにも多すぎるのです。少し極端な例かもしれませんが、三目並べ(別名、○×ゲーム)と比較して考えてみましょう。
三目並べの場合、ゲーム中に現れる「○と×の並び方」のパターンはどれほどあるか分かるでしょうか? 全部で9つのマスがあり、それぞれのマスは、○、×、空白のいずれかを取ります。したがって、単純な組み合わせで計算すると、3の9乗で19,683通りになります。ただし、この中には、全部のマスが○と言った、実際にはあり得ない盤面も含まれます。ゲーム中に現れる盤面に限定すると、その数は3,793通りにまで減少します(本当に確認しましたよ!)。
囲碁と三目並べの本質的な違いとは?
この程度の数であれば、盤面の状態がどのように変化するかというすべてのパターンを「樹形図」として表すことも不可能ではありません。もちろん、実際にノートに書き表すのは大変ですが、コンピューター上で樹形図全体の情報を構成して、メモリーに記録することは可能です。ちなみに、樹形図の情報を表すデータ構造と言えば……これは試験に出るポイントですね(笑)。冗談はさておき、仮にそのような樹形図がメモリー上に構成できれば、これは、必勝法がわかったも同然です。樹形図をたどっていき、自分が勝利する状態に繋がる手を打ち続ければよいのです。三目並べの場合は、お互いに最善手(その盤面におけるベストな手)を打ち続ければ、必ず引き分けになりますので、「必勝法」というのは誇大広告かも知れませんが……。
三目並べの樹形図のイメージ
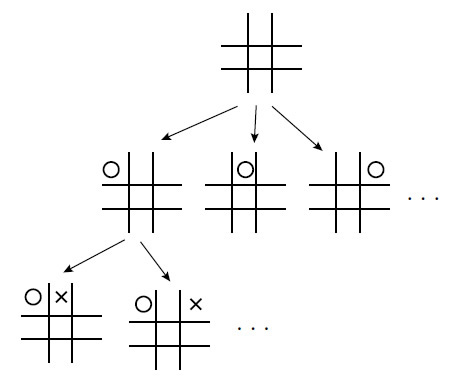
それはさておき、このような三目並べの必勝法をプログラミングする方法は実際に知られており、「動的計画法」と呼ばれる最適化アルゴリズムを適用することで、最強(?)の「三目並べエージェント」を作ることができます。詳しい内容は割愛しますが、このアルゴリズムを用いると、盤面 sにおいて次の手 aを選択した時に、それが「勝利」の状態にどれほど近づくかを表す関数 q(s, a)(これを「行動-状態価値関数」と言います)が決定できます。つまり、盤面 sにおいて、q(s, a)が最大になる手 aが最善の手になるのです。この方法であれば、毎回、樹形図を最後まで「読み切る」必要もありません。あらゆる盤面に対して、その状況における最善手を示した「チートシート」が用意されていると思えばよいでしょう。
それでは、これと同じ方法を囲碁に適用するとどうなるでしょうか? 原理的には、まったく同様にして最強の囲碁エージェントを作ることができるはずですが、現実にはそうはいきません。囲碁は、取り得る盤面の数が多すぎるのです。一説によると、対局中に現れる盤面のパターンは、10の127乗よりも多いそうです。1ペタバイトは10の12乗バイトですから、これだけの数の盤面を記憶できるメモリーはこの世には存在しません。「樹形図記憶作戦」は、この時点で破綻するのです。
……なんだか残念な感じになりましたが、いえいえ、決してそんなことはありません。コンピューター囲碁プレイヤーや、人間よりも上手にビデオゲームをプレイするエージェントなど、人間と対等に競える力を手に入れるコンピュータープログラムの事例は着実に増えています。ここで利用されるのが「強化学習」の手法です。この強化学習の根本原理は、先ほどの三目並べの例とさほど大きくは違いません。状態の数があまりにも多いため、すべての場合を網羅して、「行動-状態価値関数 q(s, a)」を厳密に決定することはできませんが、なんらかの方法で、近似的に q(s, a)を求めるのです。あるいは、樹形図のすべてを真面目にたどるのではなく、「おそらく勝利に近いだろう」と思われる部分だけを選択的に調べるという方法もあります。
『ITエンジニアのための強化学習理論入門』では、このような「強化学習の根本原理」を基礎から丁寧に解説しています。すべての場合を網羅した「厳密解」を求める動的計画法のアルゴリズムから始まり、状態数が多すぎて厳密解が求められない場合の近似法へと段階を追って説明していきます。これらのアルゴリズムをPythonのコードで実装して、「なるほど、だから強化学習はうまくいくのか!」と実感してもらうことが本書のゴールです。
子供の頃に遊んだ(?)
「あるけあるけゲーム」

私と同世代の方であれば、子供の頃に「パソコン」で遊んだ「あるけあるけゲーム」を覚えているかも知れません。本書の最終章では、ニューラルネットワークを使った強化学習のテクニック「DQN」で、このゲームをプレイするエージェントを実装します。強化学習ライブラリーをブラックボックスとして使うのではなく、「ちゃんと中身を理解して使いたい」というあなたのための一冊です。



