会社の仕事や家庭の営みなど毎日落ち着かない。そのような日常から離れた世界を覗く楽しさがある。日常からの知的離脱の一つとして相対性理論は恰好の世界です。啓蒙書はさまざまあるのですが、どれもあるレベルで終わっています。これは一般読者を見下しているのではあるまいか？ 一方で深いりすると、一般相対性理論では、テンソル記号が紙面いっぱいに広がっています。幾何とは言いながら、直線と曲線による線画に代わって符号の羅列でありうんざりさせます。著者あるいはタイプセッターによるエラーが無いとは言えないのが心配です。

本書はできるだけ幾何らしく図版を入れました。自信をもって言えるのですが、啓蒙のレベルを超えて本質に迫っています。

相対性理論の素晴らしさは、奥深さにあります。フィクションではなく真理に迫るからです。それは直線と直角の関係から始まり、宇宙の構造と幾何の関係に焦点を当てています。英語やドイツ語と違ってこの2つの基本語直線と直角は要を得ています。

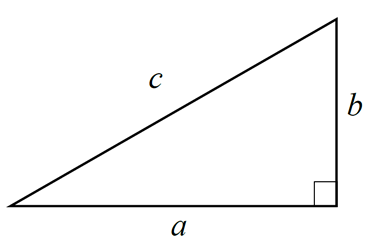
ピタゴラスの定理は

で表されます。

ここで、身近な太陽系（あるいは太陽よりもずっと大きな恒星）の惑星の動きを語るときの自然な発想として、太陽の中心から遠方は距離$r$が大きいほど（遠方ほど）重力の影響が小さくなると考えます。そこで$r$に代わって$u=1/r$が距離を表す変数としてみます。つまり逆数です。図2のように、ある基準軸からの位相角を$\phi$とします。

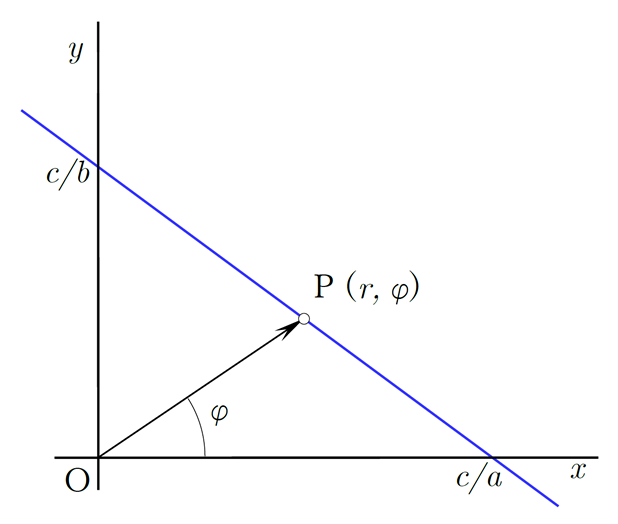
そして次の式を提示します。

これはピタゴラスの3平方の定理の形をしています。実は、これがユークリッド幾何であることを本書の第1章で主張しています。というのは、大学や高校の数学で、自分の位置を通らないいかなる直線もこの式に従うからです。微分を含むこの3平方の式は直線の方程式なのです。ユークリッドの時代には微分・積分の概念がありませんでした。

ところが、この方程式には特異解として1個の円が存在します。ユークリッド幾何の2つの要素である直線と円が含有されているのが不思議です。この式の発見に関与した本書の2人の著者の役割はこのようなものでした。さまざまな模索中に(2)式が直線を表すことを見つけたのは、数学を道具として使う技術屋の見城です。これを受けて数学的に深く考えて特異解の存在を指摘したのは、純粋数学者の佐野です。

次の3ステップ目で幅が広がります。(2)式を変形して(3)式を呈示します。

するとこれはニュートン力学での惑星の軌道式です。この式を描画すると、円、楕円、放物線、双曲線が現れます。ユークリッド幾何とニュートン力学の繋がりはここにあるのだといえそうです。

次のステップは(3)式の右辺にもう一つの項として$\alpha u^3$を加えて

とすると、どうなるでしょうか？

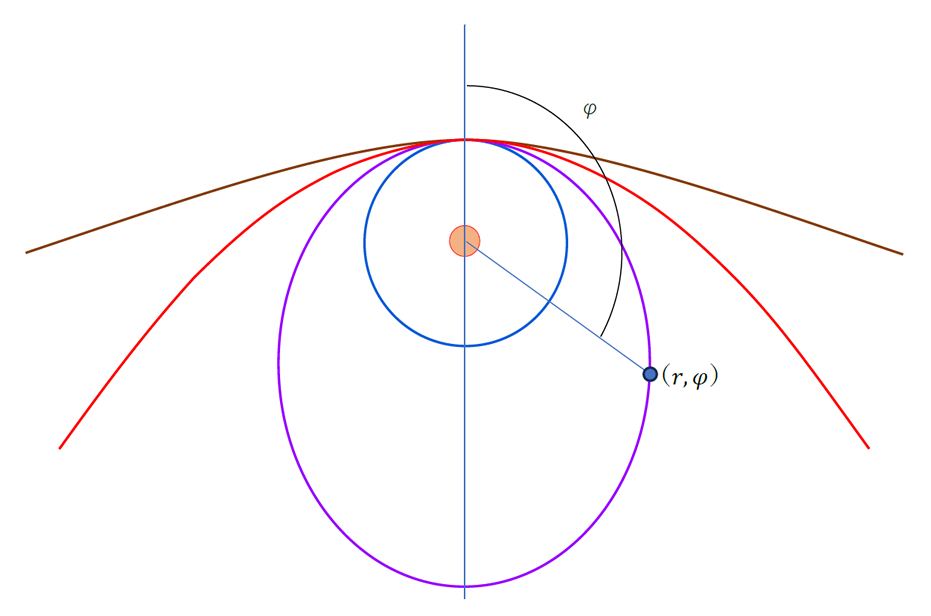
これは太陽に一番近い惑星である水星の軌道を示唆します。アインシュタインが1915年末に提唱した水星の軌道式はごたごたしているのですが、じっくりと整理したら(4)式が現れました。彼は複雑な思考と手順でこの式にたどりついたと想像しますが、説明を省いて発表を急いだように思われます。

最後のステップです。(4)式右辺第3項を左辺に移行して

• $(1-\alpha u)$: 太陽の重力による空間の歪み、ニュートン力学からのずれ、非ユークリッド幾何
• $k$: 惑星の運動量に関係、$k=0$は光跡

とすると奥深さが感じられます。ここに潜んでいる空間の曲がりあるいは歪の数式構造$(1-\alpha u)$が現れたからです。これが一般相対性理論の非ユークリッド幾何です。この方程式が描く惑星軌道はコンパスと定規ではなくプログラミングです。本書ではPythonとBASICで提示しています。17回ではこれを試すための具体的な手順を提示しました。

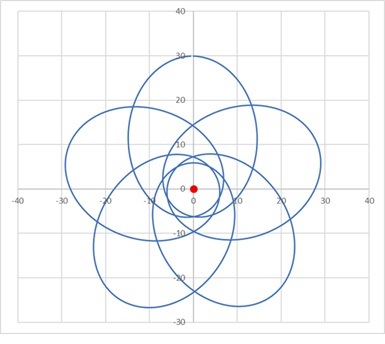
本書p.289にはExcelでこの計算をするための準備部分を記載しています。それを完成して実行した結果を図4として示します。このExcelファイルはダウンロードしてさまざまの興味深い軌道を描いてみましょう。